Plane and Solid/Surface intersection

by | Apr 9, 2020 | Blog, Revit Programming | 0 comments

So far we discussed Plane-Plane, Plane-Line and Plane-Curve intersections. None of these methods were not found in REVT-API and you had to find a work around to implement them yourself. The same applies to Plane-Solid intersection which we discuss in this post. The closest method you can find in Revit-API is the CutWithHalfSpace() method:

public static Solid CutWithHalfSpace(
	Solid solid,
	Plane plane
)
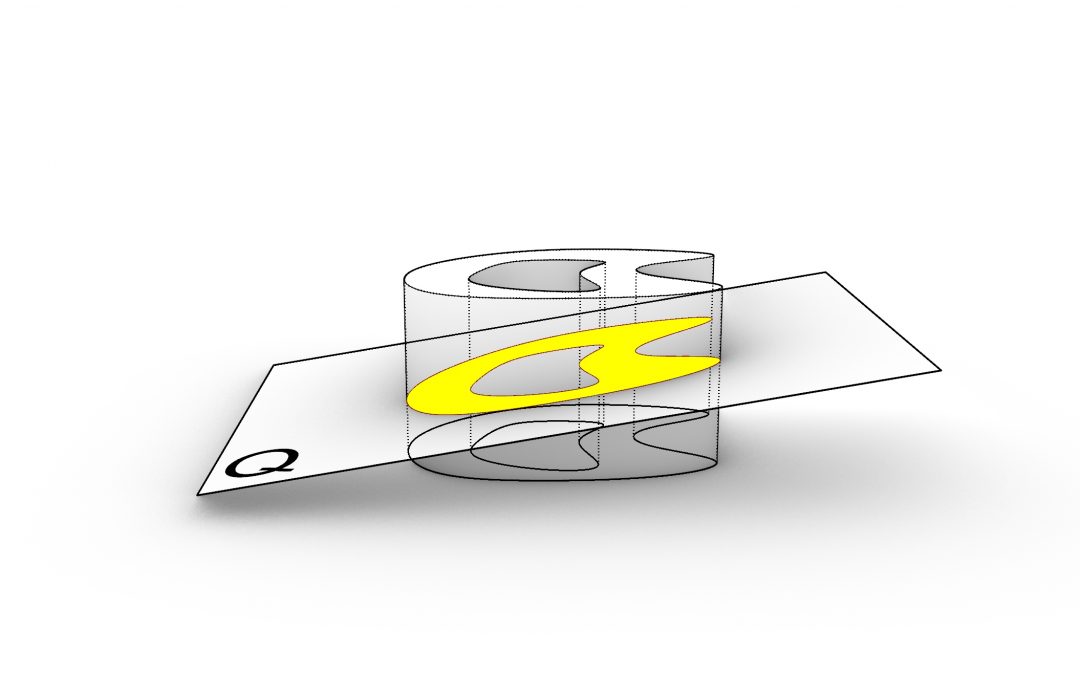
Above creates a new shell by removing the portion of the input solid which falls into the positive space of the plane.If nothing is generated then we must check the negetive the space by flippong the plane.This operation (if plane actually intersect the object) creates a new set of curves within the cut plane. All we need to do is to extract those curves. If the input geometry is a solid poly-surface then the intersection is expected to be multiple set of the Curve loops and if the geometry is a surface then a single curve or line may found.
We search in the Edges of the resulted geometry for the curves that are coincide with the input plane. In case of the line (Plane and planar surface) we need to search for a curve which is within the input plane. This can be done using the Plane-Line intersection method we developed earlier. The line lies in the plane If the result of the intersection is Sunset : 
if (curve is Line)
{
    // check if the line lies on the plane 
    Line l = curve as Line;
    if (plane.Intersect(l,threshold,out XYZ p,out double t)== Plane_Line.Subset)
        intersections.Add(curve); // add curve to the intersection list of it lies on the intersection plane
}
If the edge is a curve we must check if it is planar. In Revit API there is no direct method to check the planarity of the curve, however, if you build a CurveLoop from the curve then you can use methods to check (HasPlane()) and retrieve the plane (GetPlane()) of the curve. Once the of the curve is available we can find out whether it is coincide with input plane or not. For this we use the IsCoincident() method that we have implemented before.
// add the curve to an empty CurveLoop to find out if the curve is planar
CurveLoop cl = new CurveLoop();
cl.Append(curve);
// if curve is planar then check if the plane of the curve is coincident with intersection plane 
if (cl.HasPlane()) 
{
    Plane pl = cl.GetPlane(); // retrieve the plane of the curve
    if (plane.IsCoincident(pl, threshold))
        intersections.Add(curve); // add curve to the intersection list of it lies on the intersection plane
}
Below is the full implementation of the method. The method returns a list of curves as result. In order to create planar surfaces from the closed chain of curves we must first create CurveLoops out of the separate curves. Note that the returned curves are not necessary in order and therefore cannot be added to a CurveLoop directly. To arrange the curves in right order we discuss an algorithm in the next post.
/// <summary>
/// Intersect this solid with given plane and return the list of intersecting curves.
/// <para>Note that curves are not in order.</para>
/// </summary>
/// <param name="solid"></param>
/// <param name="plane"></param>
/// <param name="threshold"></param>
/// <returns></returns>
public static List<Curve> Intersect(this Solid solid, Plane plane, double threshold)
{
    List<Curve> intersections = new List<Curve>();
    // cut the solid with positive side of the plane
    Solid s = BooleanOperationsUtils.CutWithHalfSpace(solid, plane);
    if (s == null)
    {
        // it could be that the plane is just on the top of the solid 
        // we cut the solid again by the reverse plane 
        s = BooleanOperationsUtils.CutWithHalfSpace
               (solid, Plane.CreateByNormalAndOrigin(-plane.Normal, plane.Origin));
        if (s == null)
            return null; // plane does not intersect the solid
    }
    // search for edges in the new solid geometry which lies on the plane 
    foreach (Edge edge in s.Edges)
    {
        Curve curve = edge.AsCurve();
        if (curve is Line)
        {
            // check if the line lies on the plane 
            Line l = curve as Line;
            // add curve to the intersection list if it lies on the intersection plane
            if (plane.Intersect(l, threshold, out XYZ p, out double t) == Plane_Line.Subset)
                intersections.Add(curve); 
        }
        else
        {
            // add the curve to an empty CurveLoop to find out if the curve is planar
            CurveLoop cl = new CurveLoop();
            cl.Append(curve);
        // if curve is planar then check if the plane of the curve is coincident with intersection plane 
            if (cl.HasPlane()) 
            {
                Plane pl = cl.GetPlane(); // retrieve the plane of the curve
                // add curve to the intersection list of it lies on the intersection plane
                if (plane.IsCoincident(pl, threshold))
                    intersections.Add(curve); 
            }
        }
    }
    return intersections; // return the result.
}

Submit a Comment