In last couple of posts (Signed distance of a point from a plane and coincident planes) I was discussing plane geometry and implementation of some properties of it in Revit API. In this post I would like to extend our discussion to the top of the intersection of plane and other geometries. For the first step we talk about the line and plane intersection and in the up-coming posts we shall discuss curves, surfaces and solids.
By definition the line-plane intersection in three-dimensional space can be the empty set, a point, or a line. It is the entire line if that line is embedded in the plane, and is the empty set if the line is parallel to the plane but outside it. As you can guess there are no such a thing as Line-Plane intersection in Revit API, however implementation of Line-Plane method is quiet easy if we just look at the algebraic definition of line and plane.
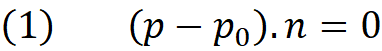
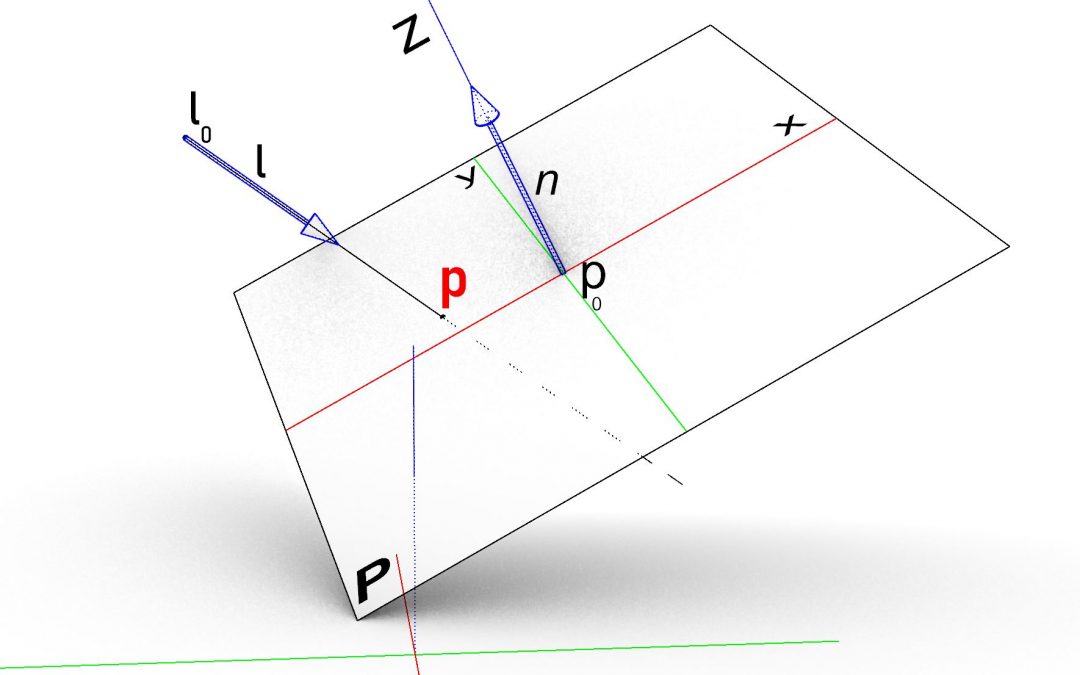
Above is an explicit equation of a plane where p₀ is a point on the plane (you may call it origin of the plane) and vector n the normal of the plane. all set of points p which satisfies above equation defines a plane in 3d space.
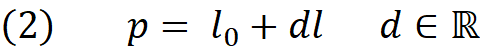
The equation 2 is the parametric representation of the line where l₀ is a point on the line, l is the direction vector and d is real number which is called parameter of the line. Note that when d changes from zero to any real number, the point p moves along the direction l staring from point l₀. Since we are interested in the intersection of line and plane we replace the point p in plane equation with its equivalent from equation (2). This is same as finding point p which satisfies both equations, meaning a point that can be on the plane and on the line simultaneously.
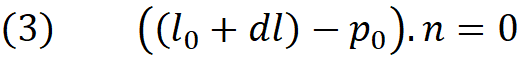
Expanding above gives us :
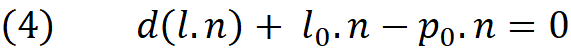
Now we solve for parameter d.
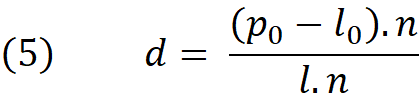
The equation (5) has a solution if the dot product of the vectors l and n is not zero. Well, in fact if the dot product (l.n) is zero it means that the line is parallel to the plane ( l is perpendicular to the n) , in this case we must check if the line is completely inside the plane or outside of it. If the line is completely indie the plane then every point on the line including the l₀ must lie on the plane. To evaluate this , we can replace p in equation (1) with l₀ and see if it satisfies the equation. If the result turns out zero (within given tolerance) then the line is a sub-set of the plane (inside it) otherwise it is outside it. We even know the distance of parallel line to the plane , and it is noting but the non-zero value of equation (1).
If the dot product (l.n) is non zero then d indicates the parameter of the intersection point on the line. To obtain the actual intersection point all we need to do is to replace d in equation (2) by its equivalent in equation (5). If we choose the l₀ to be the first point of the line then we can even find out
Let us know discuss the implementation of the Line-Plane intersection method in Revit. First we compute both numerator and denominator of the equation (5) and we check if the denominator is nearly zero :
//compute the dot prodcut and signed distance
double denominator = l.Direction.Normalize().DotProduct(p.Normal);
double numerator = (p.Origin - l.GetEndPoint(0)).DotProduct(p.Normal);
//check if the dot product is almost zero
if (Math.Abs(denominator) <tolerance)
{
// line is parallel to plane (could be inside or outside the plane)
}
else
{
// line is intersecting with plane
}
If the dot product is non zero we compute the intersection :
// line is intersecting wih plane
// compute the line paramemer
double parameter = numerator / denominator;
intersectionPoint = l.GetEndPoint(0) + parameter * l.Direction;
If not, then we check the numerator and we check whether the line is outside or inside the plane.
// line is parallel to plane (could be inside or outside the plane)
if (Math.Abs(numerator)<tolerance)
{
//line is inside the plane
}
else
{
// line is outside the plane
}
In order to represent the line-plane intersection status we can define an enum :
/// <summary>
/// The status of line-plane intersection
/// </summary>
public enum Plane_Line
{
/// <summary>
/// Line is completely inside the plane
/// </summary>
Subset,
/// <summary>
/// Line is parallel to the plane
/// </summary>
Disjoint,
/// <summary>
/// Line is intersecting with the plane
/// </summary>
Intersecting
}
Below is the complete implementation of the Plane-Line intersection method. Note that we also output the line parameter, this is useful when it is important to know whether the intersection point is inside a bounded line or not. Since we used the first point of the line .GetEndPoint(0) the intersection point is inside the line segment if the parameter is between 0 and the segment length.
/// <summary>
/// Compute Plane-Line intersection
/// </summary>
/// <param name="p">This plane</param>
/// <param name="l">Line to intersect with</param>
/// <param name="tolerance">Tolerance</param>
/// <param name="intersectionPoint">The intersection point, Null if it does not exist</param>
/// <param name="parameter">The parameter of the intersection point on the line</param>
/// <returns></returns>
public static Plane_Line Intersect(this Plane p, Line l, double tolerance,
out XYZ intersectionPoint, out double parameter)
{
//compute the dot prodcut and signed distance
double denominator = l.Direction.DotProduct(p.Normal);
double numerator = (p.Origin - l.GetEndPoint(0)).DotProduct(p.Normal);
//check if the dot product is almost zero
if (Math.Abs(denominator) < tolerance)
{
// line is parallel to plane (could be inside or outside the plane)
if (Math.Abs(numerator) < tolerance)
{
//line is inside the plane
intersectionPoint = null;
parameter = double.NaN;
return Plane_Line.Subset;
}
else
{
// line is outside the plane
intersectionPoint = null;
parameter = double.NaN;
return Plane_Line.Disjoint;
}
}
else
{
// line is intersecting wih plane
// compute the line paramemer
parameter = numerator / denominator;
intersectionPoint = l.GetEndPoint(0) + parameter * l.Direction;
return Plane_Line.Intersecting;
}
}

Recent Comments