Plane and curve intersection (2)

by | Apr 7, 2020 | Blog, Revit Programming | 0 comments

In my last my post I discussed this topic in the context of linear algebra and differential geometry. We also briefly discussed root finding method. Although the method works properly but you are probably looking for something faster! 

Here I would like to use a method from Revit API to improve the performance. 

public FaceIntersectionFaceResult Intersect(
	Face face,
	out Curve result
)

Above method compute the intersection of curve and face. If we can generate a planar face in the given plane in which intersect the curve then we can use the method to compute the Plane – Curve intersection. The question is in which position in the plane and in what size we should create the face? Let us assume that curve c intersect the plane Q at least in one point P. It is obvious that P lies in the curve c’ the projection of Curve c on the plane Q. Consequently if curve c intersect plane Q at a any point P then it also intersect curve c’, meaning the normal projection of curve c on plane Q holds all possible intersection points. Now let us take any point on the curve c , let’s say point r and find it’s projection on plane Q which is r’ a point on curve c’. From point r’ on the plane Q we draw the circle s with the radius of l the length of the curve c. We proof that circle s always contains curve c’. 

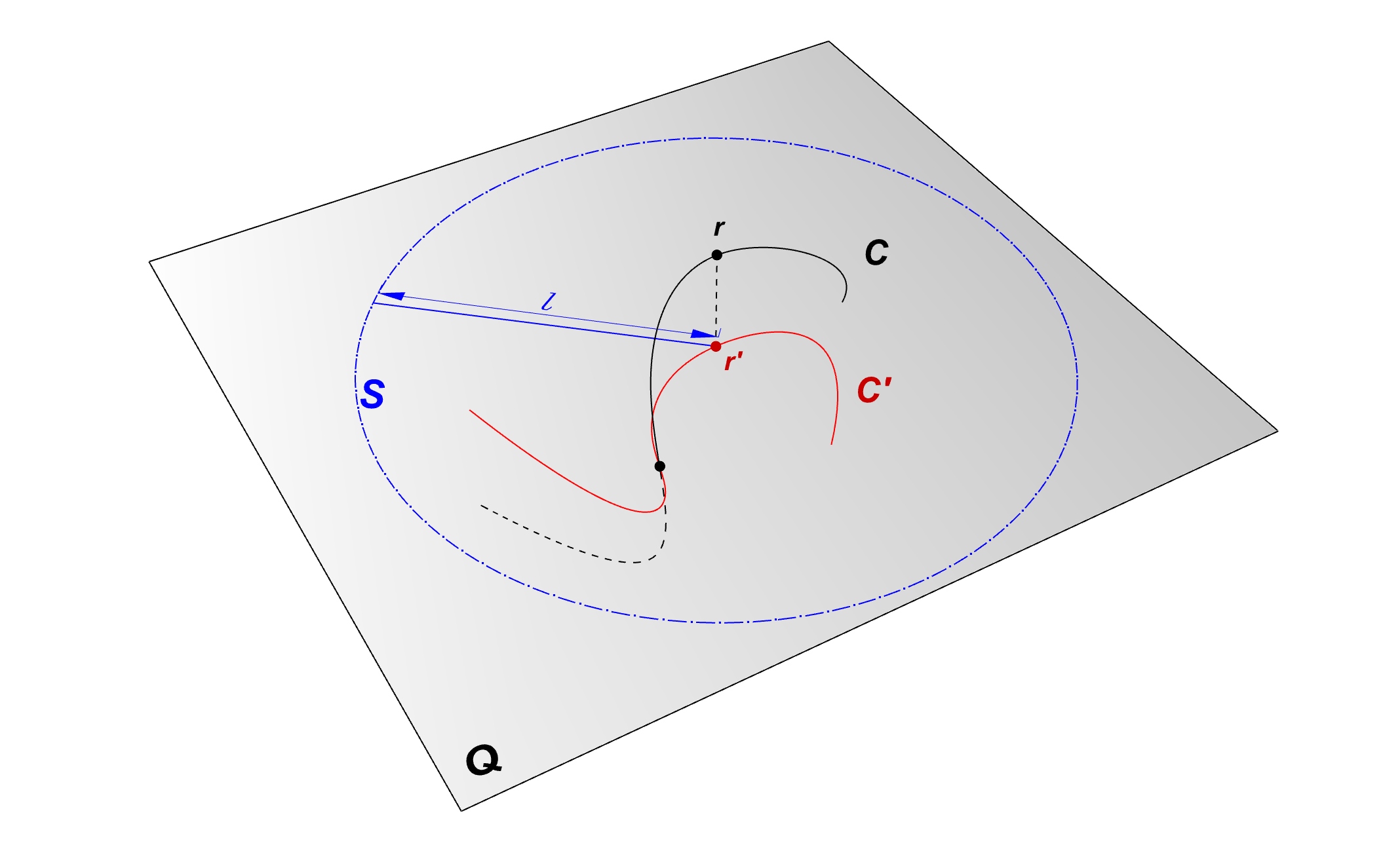
We proof by contradiction. Let’s assume the Curve c’ intersect the circle s in point x. This means the length of the line r’-x equals to l the length of the curve c. Hence we can write:

In the other hand the length of the line segment r-x’ spanning between two points on the curve c’  is shorter than the curve :

From (1) and (2) we conclude :

Above statement is incorrect , as you can see in the previous post the length of the normal projection of the curve c is less or equal to the length of the curve c. 

Now that we know a circle with the radius of L(c) around any point of the c’ includes the entire curve c’, we shall use this to construct a face of this 2l X 2l centered on a point (for example first point) of curve c’ ti insure no intersection will falls within the face. This is nothing but the bounding rectangle of the circle s as shown in below

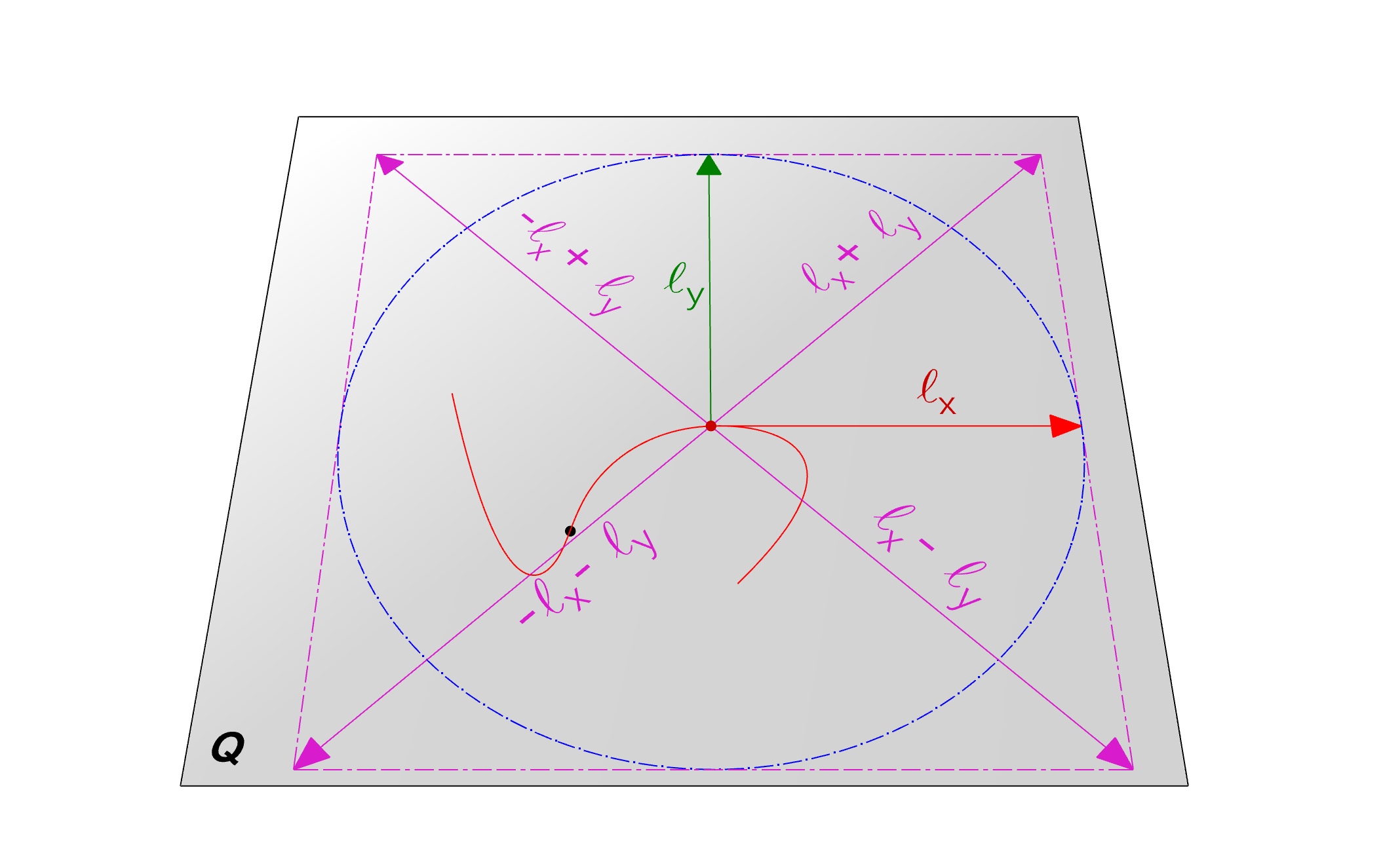
In order to build a face out of the bounding rectangle we need to use a method from GeometryCreationUtilities class.
All the methods in this class create solid geometry which makes it difficult to simply create a bounded surface (Face) , Except one method!  

public static Solid CreateLoftGeometry(
	IList<CurveLoop> profileLoops,
	SolidOptions solidOptions
)

Using above method we can create an open shell with a single face . To do so , we require a list of CurveLoops. To build a loft surface which looks like a rectangle we consider two lines either on the top and bottom or left and right side of the rectangle, CreateLoftGeometry() then generate a surface spanning between the two lines.  Below is the complete implementation. The method returns  IntersectionResultArray holding the information about the intersection events.

/// <summary>
/// Compute the intersections of the plane with given curve
/// </summary>
/// <param name="p">Plane of the intersection</param>
/// <param name="c">Curve to intersect with</param>
/// <returns></returns>
public static IntersectionResultArray PlaneCurveIntersection(this Plane p,Curve c)
{
    // Find the projection point
    p.DistanceTo(c.GetEndPoint(0), out XYZ projection);
    // construct two parallel lines l1 and l2 
    Line l1 = Line.CreateBound(projection + c.Length * (p.XVec + p.YVec),
        projection + c.Length * (p.XVec - p.YVec));
    Line l2 = Line.CreateBound(projection + c.Length * (-p.XVec + p.YVec),
        projection + c.Length * (-p.XVec - p.YVec));
    // Add lines into single CurveLoop list
    CurveLoop cl1 = new CurveLoop(); cl1.Append(l1);
    CurveLoop cl2 = new CurveLoop(); cl2.Append(l2);
    //Generate Loft surface
    Solid s = GeometryCreationUtilities.CreateLoftGeometry(
        new List<CurveLoop>() { cl1, cl2 }, 
        new SolidOptions(ElementId.InvalidElementId, ElementId.InvalidElementId)
        );
    // intersect the plane with the face (only on face is available)
    s.Faces.get_Item(0).Intersect(c, out IntersectionResultArray results);
    return results;
}

Submit a Comment